User:jim.belk/Draft:xy plane

In mathematics, the xy plane (also the Cartesian plane or the coordinate plane) is a plane whose points are identified with ordered pairs of real numbers, using the Cartesian coordinate system. Every point p on the xy plane is determined by an x-coordinate and a y-coordinate:
The x-coordinate specifies the horizontal position of p, and the y-coordinate specifies the vertical position.
The xy plane is main setting for two-dimensional analytic geometry. In higher mathematics, the xy plane is usually identified with the set R2 consisting of all ordered pairs of real numbers:
Geometrically, the xy plane is a surface (i.e. a two-dimensional manifold). It has the algebraic structure of a vector space, and it forms a metric space with respect to Euclidean distance.
Cartesian coordinates
Plane geometry
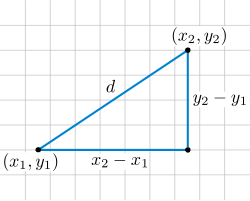
Distance formula
The distance between two points on the xy plane is defined by the formula
where (x1, y1) and (x2, y2) are the coordinates of the two points. This rule for distance follows from the Pythagorean theorem (see the picture to the right). In higher mathematics, this equation is considered the definition of Euclidean distance on R2.
Equations and subsets
Any equation involving x and y specifies a geometric object on the xy plane. For example, the equation
specifies all points on the plane with y-coordinate zero, i.e. all of the points on the x-axis. Because of this, we say that the equation y = 0 determines the x-axis. In general, any equation (or other restriction on x and y) determines the geometric object made up of those points for which the equation is satisfied
Stated differently, we can regard any geometric object on the plane as a set of possible pairs (x, y) (i.e. a subset of R2). Any rule that places restrictions on x and y a determines a set of allowed pairs, and therefore specifies a geometric object.
Lines
Any line on the plane is determined by an equation of the form
where A, B, and C are constants. For this reason, any equation of this form is called linear.
If A = 0, the equation can be reduced to y = c, which specifies the horizontal line at height c. Similarly, if B = 0 then the equation can be reduced to x = c, which specifies a vertical line.
As long as the line is not vertical, it is possible to solve the equation above for the variable y:
- .
This is called the slope-intercept form of the linear equation. The direction or slope of the line is determined by the constant m; the constant b determines the value of y when x = 0, i.e. the y-coordinate of the point where the line crosses the y-axis.

Circles and algebraic curves
A circle of radius r with a given center point consists of all points (x, y) whose distance from the center is exactly r. Using the distance formula, it follows that the equation
determines a circle of radius r centered at the point (a, b). We can eliminate the square root by squaring this equation:
- .
This is an example of a quadratic equation in x and y (i.e. an equation involving only the first and second powers of x). A general quadratic equation has the form
- .
Any curve on the xy plane determined by a quadratic equation is called a conic section. This include circles, ellipses, parabolas, and hyperbolas.
A curve determined by a cubic equation on the xy plane is called an elliptic curve. In general, any curve determined by a polynomial equation involving x and y is called an algebraic curve, while curves involving non-polynomial equations are transcendental.
Inequalities
Graphs of functions
Transformations
Vector structure
Vector sum
Scalar multiplication
Dot product
Cross product
Calculus
Neighborhoods and limits
Partial derivatives
Jacobians
Curvature of curves
Vector fields
Topology
Neighborhoods
Open and closed sets
Sequences and limits
Separation properties
Compactness and completeness
Countability, Archimedean property
Area and measure
Basic notion of area
Area formulas
Lebesgue measure
Other viewpoints
Complex structure
Projective geometry
Metrics and norms
Exotic topologies
- ^ This equation uses set-builder notation.









